Ptolemaic Astronomy in the Middle Ages
Ptolemaic Astronomy in the Middle Ages
Ptolemaic astronomy, that is, the astronomy of Claudius Ptolemy’s Mathematical Compilation, (Μαθηματικη Συνταξις) synthesized some five hundred years’ effort to account for the observed motions of the stars, sun, and planets on the assumption that their proper motions were uniform and circular and that the earth lay immobile at the center of the rotating universe. Composed around the middle of the second century C.E. and known later to Arabic and Latin readers as the Almagest, Ptolemy’s grand system had neither successor nor rival until the publication of Nicholas Copernicus’ De revolutionibus orbium coelestium in 1543. The bulk of the technical astronomy during the intervening 1400 years, both in the Middle East and in Europe, was devoted to the computation of tables and the design of instruments that translated Ptolemy’s theorems and calculations into almanacs, horoscopes, and planetaria. While Islamic astronomers carried out some systematic observations aimed at filling gaps left in Ptolemy’s work, especially in his treatment of such long-term motions as precession, Europeans concentrated on making the system accessible and useful to a variety of users.
Before the establishment of the university curriculum in Europe, Ptolemaic astronomy circulated separately from the geocentric world-picture on which it was predicated and from which it had initially taken its task. In the Timaeus (ca. 350 B.C.) Plato had first sketched out the kinetic model of a spherical earth resting immobile at the center of a vast rotating sphere containing the fixed stars and encompassing a nested series of concentric spheres each carrying one of the “wandering stars”, or planets (including the sun), along its own path through the stars. Although each sphere rotated uniformly, the combination of their separate gyrations gave rise to the appearance of irregularity in the motions of the sun and planets as viewed from the earth. Able to give a rough, qualitative account of the sun’s combined daily and annual motions, Plato left to astronomers the task of articulating the model for all the planets and of fitting it mathematically to the data that Babylonian and Greek observers had been accumulating over several centuries. That was the task that Ptolemy finally completed.
Yet, from Plato’s time on, practically no one doubted the geocentric model itself, whatever its precise fit with observational data. As Aristotle showed in greater detail in his On the Heavens, reason and common experience confirmed it. Philosophers, poets, Church Fathers, educators, and encyclopedists all spoke of the universe much as Plato had described it, embellishing his picture on occasion with the nomenclature and simpler mathematical features of technical astronomy as it was developing. Although such embellishments pointed to the astronomers’ more intricate version of the model, they did not provide sufficient detail to supplant the technical literature. They did, however, make access to that literature necessary for full understanding of the general accounts.
A socially fragile enterprise, mathematical and observational astronomy did not survive the ferment of the late Empire in the west. Until the translation of the Almagest into Latin – from the Greek in 1160, from the Arabic in 1175 – Europeans readers drew their picture of the world from the encyclopedists and the poets and hence, in the absence of any ongoing technical tradition, had neither the need for a work as sophisticated as Ptolemy’s nor the basis for understanding it. Over the next three centuries the Almagest itself circulated among a quite small number of mathematicians, while simplified versions of its contents served the wider learned audience, especially at the universities. These versions took two basic forms, De spera and Theorica planetarum.
Treatises on the sphere, of which Johannes de Sacrobosco’s (ca. 1220) became the standard, set out for students the structural elements of the geocentric universe and the rudiments of the mathematical model that accounted for its astronomical phenomena. Although the texts varied in detail, they generally opened with mathematical definitions of the sphere and with the basic metaphysical and empirical arguments that made it the shape of the earth and heavens. They turned then to the major circles that provide lines and points of reference in the sky: equator or equinoctial circle, celestial poles, zodiacal or sign-bearing circle (ecliptic), coluri (meridians through the equinoctial and solstitial points), horizon, zenith, and so on. As might be expected in a university text, the definitions were accompanied by synonyms and etymologies, the expounding of which accomplished one of the evident tasks of the sphere literature, to wit, exegesis of passages in classical and patristic literature where the various terms appear or are alluded to. For example, before explaining the rising and setting of the zodiacal constellations (and hence of the sun with them) in terms of a uniformly rotating sphere cut by a fixed, oblique horizon, Sacrobosco briefly treated three other measures of the phenomenon “according to the poets”, and even in his main discussion quoted frequently from Virgil, Ovid, and Lucan.
The motion of the sun eastward along the ecliptic combined with the rotation of the stars westward along the equator to account for seasonal changes in the length of daylight, while moving the circle of the sun’s motion slightly off-center toward Gemini adjusted for the inequality of the seasons. The resulting extremes of apogee and perigee of the sun also explained for writers on the sphere why the arctic regions are too cold, and the southern hemisphere is too hot, to be habitable; the intermediate region of habitation was divided into seven climes according to half-hour differences in the length of the solstitial day. Yet another very slow motion of the celestial sphere about the poles of the ecliptic produced the gradual drift, or precession, of the equinoctial and solstitial points eastward along the zodiac; in some accounts, e.g. Robert Grosseteste’s (ca. 1215-1230), this Ptolemaic device was supplanted by Thâbit b. Qurra’s more intricate mechanism for non-uniform precession, or trepidation (see below).
With the kinetic model established for the sun and stars, treatises on the sphere turned briefly to the moon and planets, the several different cycles of which require more sophisticated arrangements of moving spheres and the use of two new devices, the epicycle and the equant. These lay at the heart of Ptolemaic astronomy, constituting both the basis of its precision and the point of its departure from strict geocentrism. Yet, precisely here writers on the sphere hurried through their presentations. “Every planet except the sun has an epicycle”, wrote Sacrobosco, “and an epicycle is a small circle along the circumference of which the planet is borne, and the center of the epicycle is always carried along the circumference of the deferent.” Simply introducing the names of the devices and their components in this manner, he could do no more than suggest vaguely how they were related to the phenomena they saved, in particular to the retrograde motion of the planets and to eclipses of the moon and sun.
As part of the arts curriculum, the tracts de spera represent what most educated people knew – or were supposed to know – about Ptolemaic astronomy. They set out the vocabulary and conveyed a general, qualitative sense of how the basic mathematical devices explained the celestial appearances. But they provided neither demonstrations of the mathematics nor instructions for linking the devices to the observational data contained in the various astronomical tables. For the demonstrations the curious student of the thirteenth or fourteenth century still had to seek out the Almagest itself; for instructions he could turn to readily accessible abridgements generically titled, “theory of the planets”.
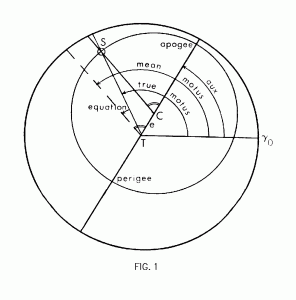
The theory began with the model of the sun’s motion familiar from de spera (Fig. 1). The sun moves uniformly in the plane of the ecliptic along the circumference of a circle of which the center is displaced from the center of the world along the apsidal line joining apogee and perigee (the points of slowest and fastest motion, called here the aux and oppositio augis respectively). The two centers of reference give rise to two measures of the sun’s motus, or longitude along the ecliptic from the conventional starting point of 0o Arietis (vernal equinox). The mean motus about the center of the eccentric increases uniformly at a rate fixed by dividing 360o by the length in days of the solar year. The true motus about the earth differs from the mean by an amount called the “equation of the sun”, which varies over the year as a function of the mean motus and which depends as well on the eccentricity (the distance e between the two centers) and on the longitude of the apsidal line. Values for the mean motus and the equation were contained in the astronomical tables, and their sum (or at times difference) gave the true motus.
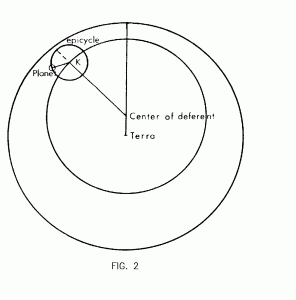
The moon and planets required much more intricate arrangements, fundamental to which was the epicycle (Fig. 2). The body was taken to move on a small circle, the epicycle, the center of which itself moved on a circle, the deferent, around the center of the world. In most cases the deferent was an eccentric circle like that of the sun. In the case of the moon (Fig. 3), the eccentric deferent itself constituted a large epicycle turning on a smaller deferent centered on the earth. From a starting position of conjunction with the sun, the center of the deferent revolved from east to west at about 11o a day, the center of the epicycle from west to east at about 13o a day (with respect to the earth), and the moon on the epicycle in the same direction as the deferent at about 24o a day. (As a result of the first two motions, the mean sun always lay midway between the center of the moon’s epicycle and the apogee of its deferent.)
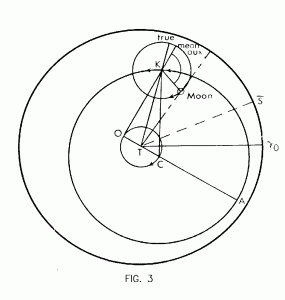
Uniform motion on the epicycle (mean argument) was measured from its mean aux, a point determined by a line drawn from a point opposite the deferent’s center on its small circle. When added to (or, during half the cycle, subtracted from) the “equation of center”’ or difference between mean aux and true aux (determined by a line from the earth through the center of the epicycle), the mean argument was transformed into the true argument. The last then led to an “equation of argument” which, added to the mean motus of the epicycle’s center, in turn yielded the true motus of the moon. Again, mean values and equations, which depended on mathematical calculations using the moon’s fixed parameters, could be found in the tables.
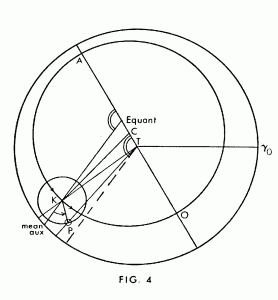
The three “outer” planets (Mars, Jupiter, Saturn) each had a fixed eccentric deferent, but the motion of the epicycle’s center from west to east along it was made uniform with respect to the center of another circle, the equant. That center lay on the apsidal line joining the earth and the center of the deferent (Fig. 4).
The line from the equant’s center through the epicycle’s determined the latter’s mean aux, from which the mean argument of the planet was measured, increasing from west to east Otherwise, the parameters of the planet’s motion were defined as in the moon’s model, except that the equation of argument and the equation of center were always equal. Two additional points did require special identification on the planet’s epicycle, to wit, the points on the bottom half between which the planet’s speed in moving eastward counteracted the epicycle’s westward swing along the deferent, thus making the body as seen from earth stop, move eastward, stop, and then resume its normal westward motion. These points of station bounded the arc of retrograde motion.
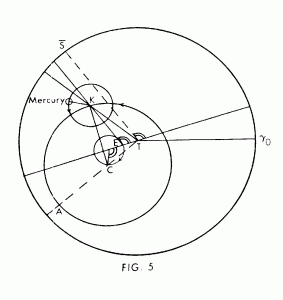
To account for the fact that Mercury and Venus (the “inner” planets) remain always within fixed distances from the sun, the center of each epicycle was taken to move about the equant with the mean motus of the sun. Revolving about the epicycle at a uniform rate determined by the period of conjunction with the sun, each planet moved away from the latter to a fixed limit and then moved toward it again, first to one side, then to the other, in an exaggerated form of retrograde motion. Although Venus’ model otherwise looked like that of an outer planet, Mercury’s had a moving eccentric like the moon’s; the center of the deferent revolved about the circle centered on the line of apsides and passing through the center of the equant (Fig. 5).
Ptolemy’s needlessly intricate mechanism for dealing with variations in planetary latitude north and south of the ecliptic received scant attention in medieval theory. The plane of the moon’s deferent and epicycle was inclined to that of the ecliptic, and the line of intersection joining the nodes (called the “head and tail of the dragon”) was rotated in the ecliptic by a separate motion of the moon’s heaven. In the planetary models, the deferent was inclined to the ecliptic at a fixed angle, while the epicycle’s inclination to the deferent varied from a minimum at the nodes (where the epicycle lay in the plane of the ecliptic) to a maximum at quadrature.
Equally problematical to medieval writers was the phenomenon of precession, in which a minute difference between the lengths of the solar and sidereal years causes a very slow motion of the equinoctial points, and consequently of the planets’ auges along the ecliptic. Ptolemy had explained it by giving the sphere of the stars a motion in consequence about the pole of the ecliptic, thus producing a steady eastward drift of the auges. But in a study widely available in translation as De motu octave spere, the ninth-century Arabic astronomer Thâbit b. Qurra proposed an oscillating model to account for what he thought was a periodic variation in precession, called “trepidation”. The theorica cited both theories, leaving the choice to the reader.
Following the pattern of the Almagest, then, each model of the theorica planetarum analyzed the “true” appearances from the earth into a composite of mean motions and compensating equations and conversely showed how such parameters translated into actually observable measurements. But while the Almagest also provided the apparatus for calculating those parameters from the observational data combined with the mathematics of the models (and thus, incidentally, for tinkering with the models), the theorica assumed that readers had access to on e of the various tables that by the Middle Ages circulated separately from their prototype in the Almagest and that reflected in the mixed provenance of their data the subsequent touch of Italian and Islamic hands.
Belonging to an independent genre, a set of tables (called a zîj in Arabic) had its own accompanying instructions, or canons, and could be used without reference to the models. The first tables to enter Europe stemmed from the ninth-century Arabic astronomer and mathematician al-Khwarazmi; rendered into Latin by Adelard of Bath in 1126, they were subsequently adjusted for the Christian Era and for various European meridians. Somewhat later they were joined by another set, the Toledan Tables, generally (but uncertainly) ascribed to the eleventh-century astronomer al-Zarqal; (Arzachel), whose translated canons were particularly popular. In the 1260s Alfonso X of Spain ordered the compilation of tables designed to be universal; preliminary calculations allowed the user to adjust for meridian and epoch. Extant only in the form given them by Johannes de Lineriis and his student Johannes de Saxonia in Paris in the 1320s, and generally accompanied by the canons of one or the other editor, the Alfonsine Tables remained the standard for European astronomy until the sixteenth century.
Using the tables with an understanding of the models behind them was made easier by versions of the theorica planetarum that translated the models directly into calculating instruments. The earliest of these in the west was Campanus of Novara’s equatorium(ca. 1260), which gave instructions for assembling sets of graduated disks into physical models of the planets circles. With each disk then set from the tables to the appropriate mean motus, a planet’s true place appeared under a string stretched from the center of the instrument, through the point marking the planet on the epicycle disk, and onto the ecliptic scale etched on the rim. Inspired perhaps by Arabic instruments, the equatorium underwent improvement in the fourteenth and fifteenth centuries; in particular, Campanus’ separate models were brought together into a single mechanism allowing for all possible combinations of circles.
The replacement of mathematics by mechanics in medieval Europeans’ general understanding and use of Ptolemaic astronomy placed an emphasis on its coherence as a total structure, an emphasis reinforced by knowledge of Ptolemy’s own attempt at unification in his Planetary Hypotheses and of similar efforts by Arabic cosmologers such al-Farghani (Alfraganus) al-Bitruji (Alpetragius). Of a piece with such structural concerns, but generally critical of them, were the writings of later European cosmologers who worried about the incompatibility of Ptolemaic astronomy with Aristotelian physics. The title of a popular work of this genre by Henry of Langenstein reveals the source of the concern: De reprobatione ecentricorum et epiciclorum, also referred to in some manuscripts as simply Contra theoricam planetarum.
Ptolemaic astronomy in the Middle Ages served practical and pedagogical ends rather than theoretical ones. Writers aimed at designing tables and instruments rather than carrying out systematic observations aimed at articulating and improving the system. For the most part, it was only the astrologer who need astronomy at the time, in order to be free of the vagaries of weather and location in determining the positions of the planets. Not until the later fifteenth century, with the work of Johannes Regiomontanus (in particular his completion of George Peurbach’s Epitome Almagesti), did theoretical mathematical astronomy begin to attract scholarly interest for its own sake and bring a return to the Almagest itself. When it did, the Ptolemaic system, pressed perhaps precisely by the mechanical and cosmological concerns noted above, had only a short future.
by Princeton University
Be the first to post a message!
