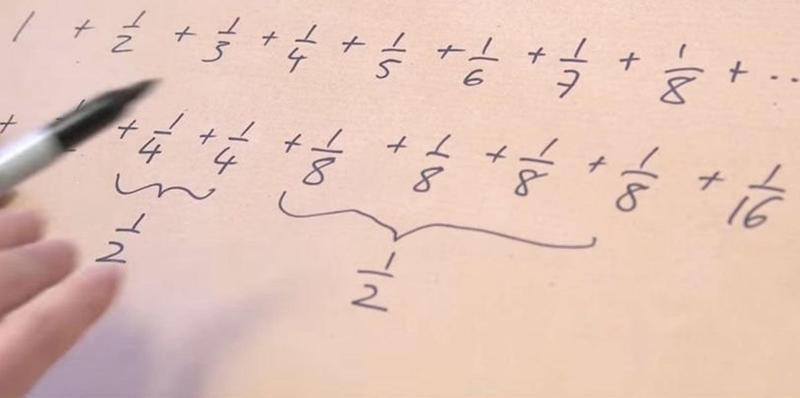The strange number 0.577 keeps showing up in everything
The strange number 0.577 keeps showing up in everything
If you had to pick the most famous number in the world, you would probably go for pi, right? But why? Despite being crucial to our understanding of circles, it’s not a particularly easy number to work with, because it’s literally impossible to know its exact value, and with no discernible pattern to its digits, we could continue calculating each digit of pi to infinity.
But in spite of its unwieldy nature, pi has earned its fame by popping up everywhere, in both nature and maths — and even in places that have no clear connection to the circles. And it’s not the only number that has a rather eerie ubiquitiousness — for some reason, 0.577 keeps cropping up everywhere too.
Known as Euler’s constant, or the Euler-Mascheroni constant, this number is defined as the limiting difference between two classic mathematical sequences: the natural logarithm and the harmonic series.
The harmonic series is a very famous series of numbers that you get if you start adding up numbers like this: 1 + 1⁄2 + 1⁄3 +1⁄4. Continue that to infinity, and you’ve mastered the harmonic series.
The natural logarithm is far more complicated to explain than that, but the tl:dr version is if you take the difference between the values of natural logarithm and the harmonic series, you’ll end up with a finite number called Euler’s constant, which is 0.577 to three decimal places (and just like pi, it can go on into many, many decimals - around 100 billion).
What the number 0.577 can explain is something truly mind-boggling.
Imagine you have a circle with a circumference of 1 metre, and you put an ant at the top, and it starts travelling around the circle at a constant rate of 1 cm every second. Then imagine that while the ant’s doing its thing, you’re expanding the circumference of the circle by 1 metre every second.
So every second, the ant is making 1 cm of progress around your circle, but you’re adding 1 metre to the length of the journey. There’s no way the ant will every make it all the way around the circle, right?
Incredibly, that’s wrong. The ant can actually make it all the way around the circle when travelling at a constant rate, despite the fact that you keep adding to it, and the reason why is that the distance in front of it isn’t the only thing that’s increasing — so is the distance behind.
Of course, by the time our ant makes it all the way around, the Sun will have burnt out, so we’re talking about a series of numbers that grows almost unfathomably slowly.
That’s interesting in itself, but what’s perhaps even weirder is that Euler’s constant isn’t just involved in explaining that seemingly paradoxical riddle. It shows up in all kinds of problems in physics, including several quantum mechanics equations. It’s even in the equations used to find the Higgs boson.
And no one has any clue why. I’ll let the Numberphile video below explain that one to you, but let’s just say we’ve never thought of numbers as being so uncomfortably spooky as much as we do right now:
by Jonny Anomaly and Brian Boutwell/Quillette
Be the first to post a message!