I buried a box underneath the sand on a remote Japanese island four years ago, containing a message, an item of mine, and a question scrawled spontaneously on a tiny piece of paper. It remained above the high tide mark of the azure, almost untouched waters for years.

Why did I bury it? I liked part of the mystery, the novel-esque thought of recovering a secret box years down the line, and handing it to someone important to me, passing on another little tale in a rather eccentric life to a curious human spark.

Another way of looking at the reasoning behind the burial of the box was espoused by the philosopher Nietzsche a few hundred years ago: “Those who were seen dancing were thought to be insane by those who could not hear the music”.

It was this particular passage from the aforementioned philosopher, overheard accidentally in a café in far-away California, which inspired the thought of burying something secret in an unusual place for a future friend to find. A coincidence spread across centuries led to this small change in my life; what effect would burying this box in the sand have on my own future, or someone else’s? What cascade of coincidences and events did I begin by overhearing that passage by Nietzsche?

From an individual perspective, this seems to be an entirely random series of events. But looked at over a long period of time, and tracking the branching changes in the planet that follow from it, all the chaos does produce a form of identifiable order. Patterns will appear out of the chaos. And this, in its essence, is chaos theory: finding order in the chaos.

Chaos theory was immortalized in fiction by “The Sound of Thunder,” a short story that tells the tale of a contemporary presidential election being affected significantly by the death of a pre-historic butterfly. The chain of coincidences that led to this altered future seemed to be random and unpredictable, but when all the changes are tracked-a gargantuan, realistically impossible undertaking-order does emerge. The problem is, you have to accept the idea of chaos trumping simple cause and effect first, before you can see the inherent order at all.

Chaos theory falls into that category of scientific ideas that few actually understand but many have heard of, due to its expansive, epic-sounding principles and thoughts. Who wouldn’t love to write a scientific paper entitled “If a butterfly flaps its wings in Brazil, does it cause a tornado in Texas?” Inherent to the theory is the idea that extremely small changes produce enormous effects, but ones that can only be described fully in retrospect. Accurate prediction is somewhat impossible. There are many great examples of this in nature, and climate change is one of them. Small atmospheric changes in one part of the globe can produce enormous effects years later in another region, thanks to the system feeding back changes into itself. Think about heating the planet by one degree Celsius. This increase in temperature will, due to a quirk of chemistry, reduce the ability of the world’s oceans to hold carbon dioxide. Carbon dioxide will leak into the atmosphere as a result, which will heat the planet. This will feed back into the climate system and cause more carbon dioxide to leak from the oceans into the atmosphere. If the cycle begins to self-sustain, without any additional input from another source, a runaway global warming effect will occur-the same kind of process that turned Venus into a 900-degree oven.

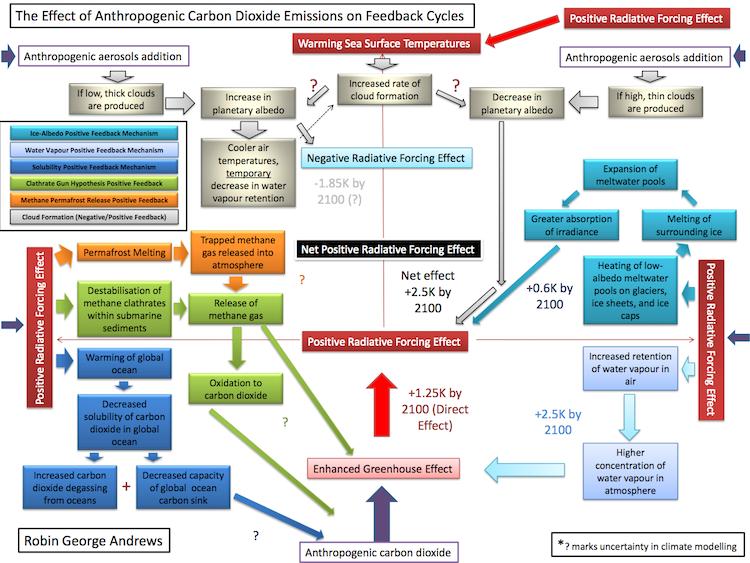
Just to illustrate the chaos of such a small change, here’s a diagram-an extremely oversimplified one based on the 2007 IPCC report on anthropogenic climate change-illustrating some of the chaotic feedback cycles operating on the planet today, and how they would respond to a small increase in global temperature. There is order emerging from the chaos, but we can only say roughly which direction the temperatures will change, not precisely by how much.

Chaos theory applies even to economics. For example, when the Betamax-a video recording format by Sony-was released alongside the VCR, traditional economists thought that it would divide the market in half, as both had the same recording capabilities of the other. However, how many of you have heard of the Betamax? Exactly: the VCR tape system overwhelmed the market (until the DVD appeared at least). Why? Well, the recording time of the VCR was ever so slightly longer, and so people could record not just television programs, but feature-length films. This very small change created a huge amount of chaos and unpredictability, and led to the market dominance of the VCR.

Or imagine a water faucet being turned on gradually. The water would flow fairly smoothly, with very little variations in the flow. Increasing the flow of the tap tends to increase what fluid mechanics calls turbulence: The seemingly random fluctuations in the flow pattern of the water. Putting the tap on full blast would create a messy, chaotic flow of water, with seemingly no discernable pattern. This turbulence, however, must be controlled by a variety of simple factors: the speed of flow, the pressure of the water system, the atmospheric conditions, the shape of the tap, and the volume of water. However, despite looking like a simple system, it rapidly becomes unpredictable. Its behaviour, nevertheless, isn’t random. It’s just essentially impossible to predict. In rare instances, we notice the flow smooths itself out, when all the conditions of the system are at certain values or positions, and a temporary order is produced. In very basic terms, if you plot this hypothetically infinite number of variations on a graph in infinite space-called phase space-you produce self-completing spirals patterns, called strange attractors. There is chaos throughout the graph except at few, infinitesimally small points, wherein order is found.

Throughout the universe, there are systems that, despite being inherently chaotic and unpredictable, tend to naturally become ordered. They fight against the inexorable entropic increase of the universe-the overall trend of every system to go from an ordered state to a disordered state. Chaotic systems sound like systems destined for disorder and destruction, so where’s all this self-organizing, self-preserving order emerging from?

One leading idea is that these strange attractors-small periods wherein order forms from chaos cancelling itself out temporarily-exist everywhere, from the formation of galaxies due to initial chaotic instabilities in the formation of the fabric of space-time, to the honeycomb-esque arrangement of bubbles rising to the surface of a carbonated drink. There are a myriad of examples of self-organizing systems in nature, but a particularly interesting one to me is the three-body problem.

The three-body problem is as follows: imagine three moons orbiting a planet. The gravitational forces from the planet keep the moons in orbit, but what effect would each moon’s individual gravitational field have on the other moons? If they orbited in a regular pattern, the small perturbations of one moon on the other might gradually pull one out of its orbit and cause a huge impact event as two of the moons crashed into each other.

Take the Galilean moons of Jupiter: Io, Europa, Calisto and Ganymede. If the orbits of these four, fairly proximal moons followed a regular, periodical orbit, their orbits would be perturbed gradually by each other’s gravitational fields, and they would impact each other. However, mathematical models suggest that this will not happen. As it turns out, the orbital periods of the moons are quasi-periodical, meaning that the orbital patterns do not precisely repeat themselves each time. The inherent chaos of the system, formed by nothing more than easily deterministic gravitational parameters, cancels itself out-a planetary-sized strange attractor-to produce a stable, self-organized orbital system. Once again, there is order emerging from the chaos.

Back on Earth, the near-infinite variables of weather systems across the planet appear stable when looked at from a distance. We call this particular form of chaotic order, this enormous strange attractor, our climate.

Life itself is an expression of self-organizing systems: profound considering the unconsciousness of the processes that led up to the formation of life in the first place. But for human beings, the improbable profoundness of chaos theory goes even deeper.

The neurons in your brain only fire in response to another electric signal firing at them. If each neuron represents a self-enclosed one-dimensional object-in a space with billions of one-dimensional objects-then your brain has a hypothetical billion dimensions within it. So when one neuron fires, the path may be initially deterministic, but the cascade of electrochemical transmissions rapidly becomes unpredictable. From ten billion neurons, or dimensions, a single thought generates a hypothetically infinite number of chaotic paths. However, this process is not random - it is merely chaotic. So what if consciousness itself is a point of time, frozen for examination, within this space? What if your personality is where the chaos occasionally settles, in a strange attractor?

Chaos is something that, biologically speaking, can be quite healthy for you or quite dangerous, depending on the organ. If the electric signals in your heart show signs of chaos and unpredictability, this can lead to a heart attack. On the other hand, an epileptic seizure is nothing more than a pattern of abnormally periodical order in the electrochemical signals in your brain. Either way, understanding that systems are inherently chaotic, despite having simple deterministic variables, is important to coming up with conclusions as to how they will behave in the future.

Chaos theory generates another particularly wonderful question: how long is the coastline of Britain? Easy right? Why not just use a ruler to measure the coastline? But what size ruler do you use? If you made the ruler smaller, and more accurate-it would be able to measure small kinks in the coastline that you previously could not. The overall length of the coastline would thus increase using this smaller ruler. Reduce the size of the ruler even more, and even smaller kinks would be accessible; once again, the total length would increase, and so on and so on. If the ruler were infinitesimally small, the coastline would be infinitely large in size. This is an example of a fractal, another bizarre feature of this bizarre theory.

Fractals are everywhere. The branches of trees have themselves branches that, upon zooming in, would look very similar to the larger branching patterns. The nerves in your body branch out in a similar, semi-repeating way. Cities even have fractal patterns: as they develop, they branch out. When these branches gain enough of a certain critical mass - population, money, infrastructure, etc. - then they start to branch out in a similar way. Fractals are ways of seeing infinity.

Infinity does certainly imply chaos, but order once again emerges out of it. For example, the global distribution of earthquakes is known to fit a mathematical pattern. This pattern was difficult to see until someone realized the pattern was fractal. And let me ask you this: have you ever considered your life as a form of fractals?

Precisely at sundown in the desert of central Arizona, a Navajo woman once asked me, “What is your life like?” What on Earth would you say in this situation? Would you give a one-word answer, followed by a shrug? Would you perhaps describe that first person, place or overriding emotion in your mind? You could instead give a much more retrospective answer, taking the last few years of your life into account, rather than delivering a succinct linguistic payload based on the very last thing to occur to you. You could have tripped and fallen, gotten a raise, finally asked someone out, realized you left the front door open, unexpectedly thought of someone you have not seen in years that you either love or hate, failed to remember that boy or girl’s name, offended an entire nation, brought peace to a city, finished your masterpiece or ruined it, just realized that the numerical value of Pi looks like the word “pie” when seen in a mirror, discovered you have an imaginary pink rabbit following you around, or, just perhaps, you have recently stumbled across something that everyone on this pale blue dot should find out about. It all depends on how small you decide to look. Do you look at and consider each tiny individual event and wonder why they happened in isolation, or do you stand back, observe the system, and find your strange attractors, those moments you seem to settle on, and find the order in all your chaos?

Chaos theory is a difficult topic to stop thinking about. After all, even reading this article is generating chaos in both your life and your own consciousness. So if you have ever sat down after a long week, exhausted from deadlines and thoughts and considerations and hopes and regrets, and wondered why your life seems so chaotic, especially in retrospect, you can look far back in time and blame a dinosaur, or a butterfly, or perhaps a philosopher writing his imagination and ruminations on the universe down on a piece of paper. And when someone in a job interview asks you where you see yourself in five years time, point to chaos theory, and state that you could be anywhere, from joining a travelling circus as a trapeze artist to burying a box on a remote Japanese island. After all, it’s scientifically sound to say so.

by Robin George Andrews For Nature.com