Mysterious Squares
Mysterious Squares
Surely at school, university or on the Internet you have heard about the “Greek-Latin squares”, the creator of which was the Indian mathematician Sharadchandra Shankar Srikhande. Let’s look at them and the origins of his discovery.
This problem was originally discussed by the Swiss mathematician Leonhard Euler (1707-1783), shortly before his death. The Latin square is nothing more than the arrangement of n characters in an n×n array so that each character appears once in each row and column. Favorite Sudoku puzzles are also Latin squares of the size of 9×9. But Euler is not the first to talk about Latin squares.Korean mathematician Choi Seok-Jung was already an old man when Euler was first born. He also explored Latin squares, but with a different name.
In the modern world, these squares no longer seem like something magical for mathematicians, but in the time of Euler it seemed something unimaginable. Therefore, the Swiss mathematician called his work “the study of a new type of magic squares”. The difference between magic and Latin squares is such that latin squares use numbers from 1 to n and each number n times but magic squares of order n×n use each number from 1 to n² only once.
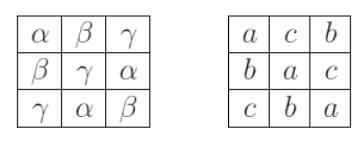
Now let’s look at the Greek-Latin squares. What the name implies is the arrangement of two sets of n characters in an n×n array, where the first set of characters comes with Latin letters, and the second with Greek letters. What is important - each pair of letters of different alphabets should not be repeated.
In his work, Euler came to the conclusion that these squares exist only for orders that are multiples of 4 and odd orders. But after a certain amount of time, his claim was challenged by Thomas Claussen (although the proof was lost), as well as Gaston Terry. They were able to make an order that is a multiple of 6. The possibility of an order that is a multiple of 2, you can try it yourself. But, most likely, your attempts will not succeed.
There is some method that allows you to build Greek-Latin squares of certain orders, using squares of smaller orders. Unfortunately, this method only works for small orders of magnitude. For example, you can take a square of order 2 and one of order 3, then the result is an order of 6. But with numbers of the form 4h+2, everything will be much more difficult, since the miracle method will no longer work.
In 1959, Srikhande, in company with RajcHandra Base and Ernest Tilden Park, destroyed the myth and published several papers showing that there are squares of orders 10, 14, 18, and others. They even created these designs in multiple dimensions! Since then, they have been called “ Euler spoilers”.
If you think that Greek-Latin squares are just fun for mathematicians and difficult tasks at the Olympiads, then you are wrong! They are of great practical importance. So, for example, they can be used in various experiments, calculating parameters, and so on.
Be the first to post a message!